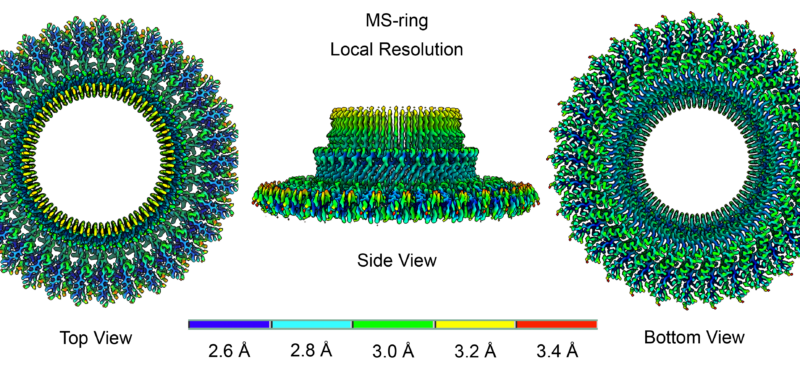
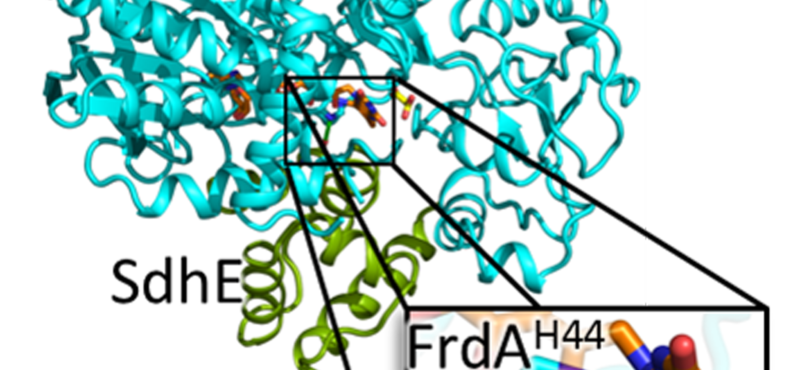
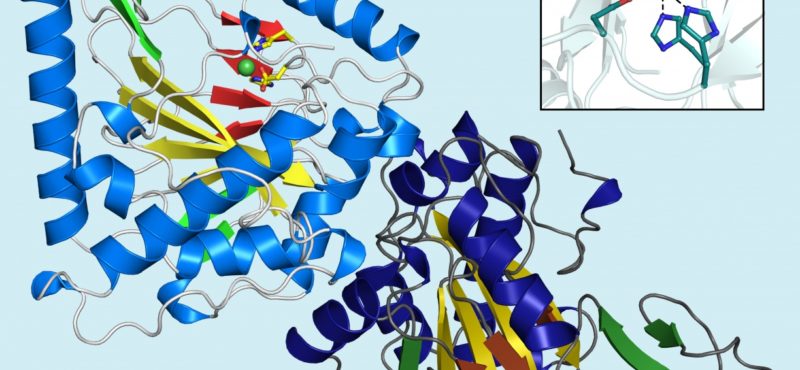
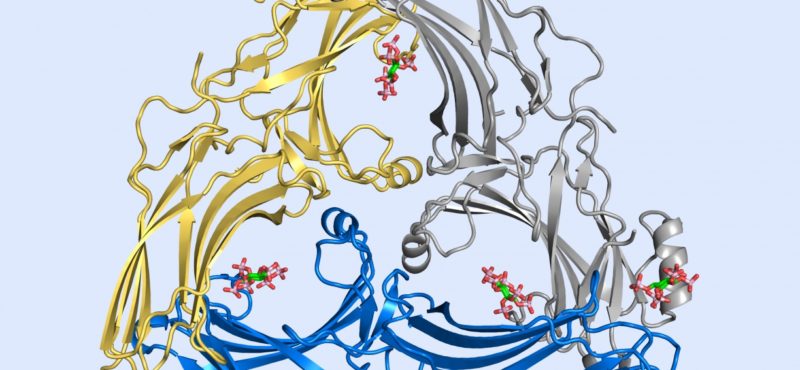
Research in the Iverson laboratory focuses on the basis for information encoding in proteins, which may manifest as molecular recognition and cellular communication. We use several model systems to understand information encoding. Research projects in our lab provide complementary information on how proteins encode information into their structures under very different biological settings. This information encoding helps bioenergetics proteins act as primordial signal scaffolds, allows mammalian signaling proteins to use conformations to select between possible outcomes, and allows hosts to recognize pathogens, and vice versa.