Numerical Modeling and Simulation and Control of Robots

Physics-based simulation and optimization-based control of walking robots treated as constrained dynamical systems that interact with their environment.

Y. Li, H. Yu, and D.J. Braun, Algorithmic Resolution of Multiple Impacts in Non-smooth Mechanical Systems with Switching Constraints, IEEE International Conference on Robotics and Automation, 2019.

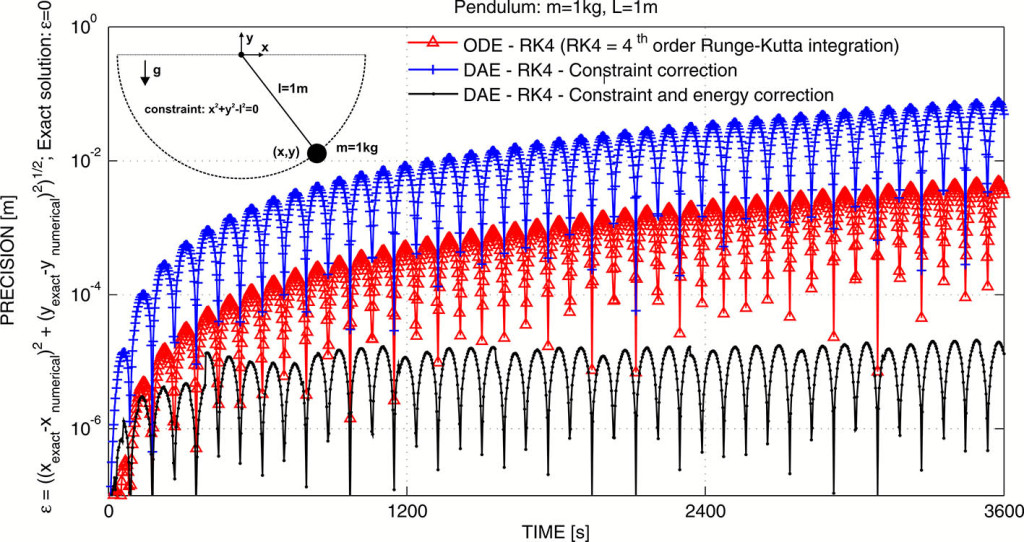
Simulation of constrained dynamical systems, modeled with differential algebraic equations (DAEs), is required in many engineering disciplines. However unlike ordinary differential equations (ODEs), that can be effectively integrated with explicit numerical methods (e.g., Runge-Kutta), integration of DAEs often requires sophisticated implicit integrators enhanced with iterative constraint stabilization. In this research, we developed an explicit numerical integration scheme which is easy to implement and can be used to accurately simulate constrained dynamical systems modeled with differential algebraic equations.

The basic assumption during the development of the integration scheme is that the computational environment is non-ideal i.e., the numerical solution is error contaminated, such that, neither the kinematic constraints, nor the energy-type conservation law, can be exactly satisfied. Using this assumption, a systematic derivation is carried out which resulted in an equation of motion that directly incorporates the correction terms required for precise satisfaction of the kinematic constraints and prevents energy drift along the numerical solution.

Importantly, the kinematic constraint correction terms and the energy correction terms are derived to be independent of each other by taking the geometry of the constrained dynamics rigorously into account. This idea enables decoupled constraint and energy correction, which leads to significant improvement in accuracy over long time integrations. The simple reproducible example below demonstrates the advantage of our method.

D. J. Braun and M. Goldfarb, Simulation of Constrained Mechanical Systems – Part I: An Equation of Motion, ASME Journal of Applied Mechanics, vol. 79, issue 4, 041017, 2012.

D. J. Braun, M. Goldfarb, Elimination of Constrained Drift in the Numerical Simulation of Constrained Dynamical Systems, Computer Methods in Applied Mechanics and Engineering, vol. 198, no. 37-40, pp. 3151-3160, 2009.